Email us

Auxetic materials: how to shrink under pressure
Author: Dr Joseph Beadle – TEAM-A Research Fellow on secondment to QinetiQ Plc.
This piece is linked to TEAM-A's 3rd Research Challenge.
Creating new and exotic materials is of interest to TEAM-A. One current investigation is exploring auxetic materials: where the Poisson’s ratio (ν) is negative. Auxetic structures have potential applications as artery dilators, a small compact device can be placed into a blocked artery and expanded to open the blockage.1 Another possible application of auxetic materials is as smart filters. Such filters have pores that change size as stress is applied. By loading such filters with medication, they can be and used as medicated bandages.2
We know that an auxetic material has a negative Poisson’s ratio, but what does this actually mean? The Poisson’s ratio relates transverse strain (εtrans) to axial strain (εaxial),
ν = -εtrans/εaxial.
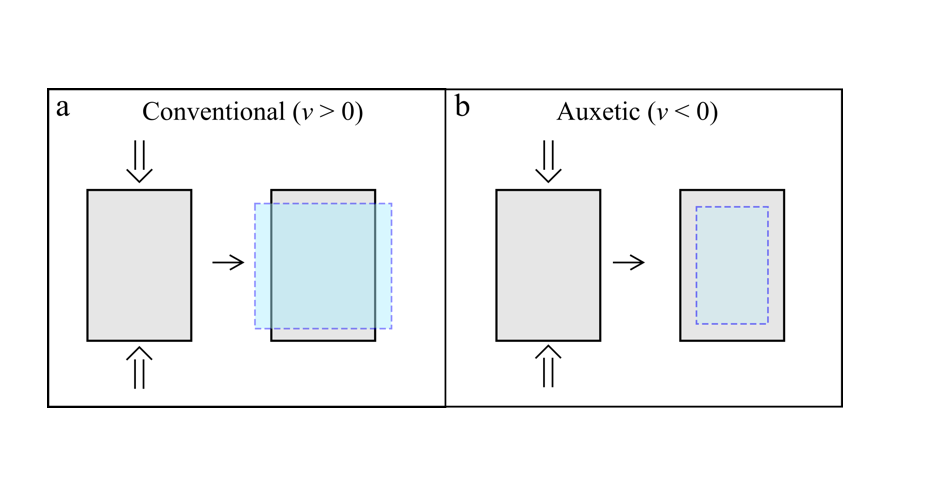
One way to visualise this is to imagine holding a cube of plastic between your thumb and index finger. As you begin compressing the plastic (applying an axial strain), you will notice that the material will expand (due to transverse strain). This expansion tells us ν > 0 for the plastic. A material where ν is close to zero undergoes little to no expansion when compressed; one such material is cork. As previously mentioned, materials where ν < 0 are known as auxetic, a term coined by Prof. Ken Evans of the University of Exeter. If you were to press an auxetic material between your fingers, it would contract rather than expand (Figure 1). The scarcity of naturally occurring auxetic materials means that we must create our own to utilise their full potential.
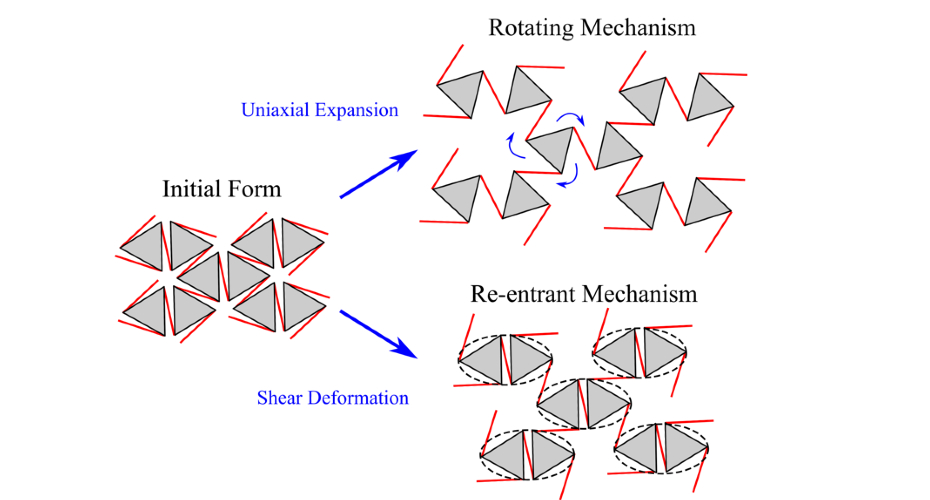
To overcome the rarity of natural auxetics, we can create materials comprised of microstructures that, when deformed, lead to auxetic behaviour. R. Lakes has described such structures.3 The author describes lattices where the unit cells are formed of re-entrant shapes, rotatable nodes linked by elastic ligaments, and some more unusual auxetic structures such as chiral structures. If we consider re-entrant and rotational systems, an example of an auxetic material that features both is presented by Mizzi et al. by using a structure with star-shaped pores.4 In this structure, a hexagonal lattice consists of two triangular-shaped patches per unit cell. Each point of one triangle is connected to another point by a thin elastic ligament (Figure 2). When the structures undergo uniaxial expansion, a rotational deformation occurs where each triangular patch rotates, resulting in a significant expansion in the transverse direction. The re-entrant mechanism occurs under shear deformation. The ligament connecting each pair of triangular patches does not deform, and all other ligaments deform. Both of these deformation mechanisms are shown in Figure 2.
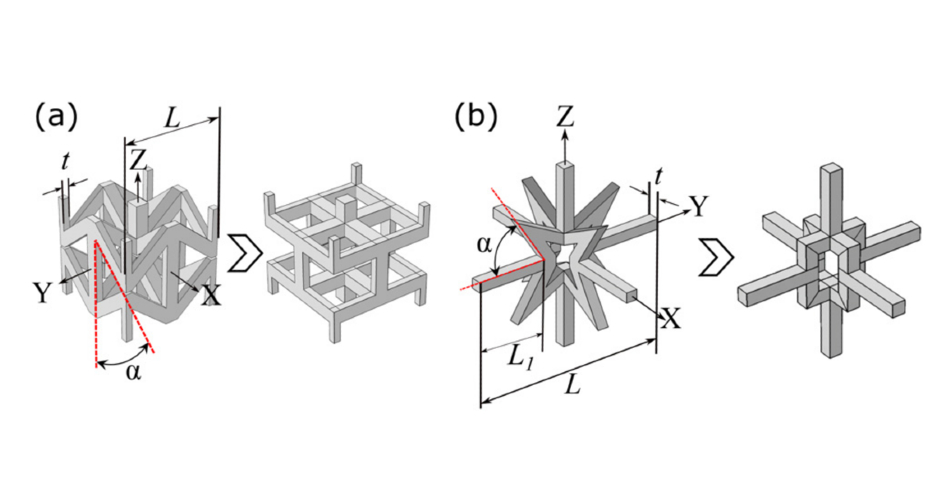
We have now seen how we can create materials that demonstrate auxetic behaviour, but how do these structures interact with propagating waves? Here, we consider elastic materials that support two polarisations of bulk waves: transverse and longitudinal. In conventional materials, the longitudinal propagate faster than the transverse. Anomalous polarisation is when the transverse wave is faster. Anomalous polarisation through 3D auxetic lattices has been investigated by G. Patil et al. through finite element analysis.5 The authors investigated the polarisation of waves at various propagation directions through auxetic lattices (structures shown in Figure 3). They showed that anomalous behaviour occurs in specific wave propagation directions, and a switch between normal and anomalous polarisation occurs under small modifications to the geometry. One significant advantage to using materials comprised of auxetic microstructures is that they function in the long-wavelength regime. The long-wavelength regime is as it sounds: the material will have the desired behaviours for any wavelength larger than the individual elements; therefore, they are broadband. This broadband nature is due to local resonances only arising when the incident wavelength becomes comparable to an individual element of the structure. Such materials have potential medical imaging applications due to the ability to accelerate and decelerate incident radiation.
Composite 3D auxetic compose of an auxetic skeleton and a filler material of a lower Young’s modulus to maintain the auxetic behaviour. Current experimental research on such structures is somewhat limited, with most research being on three-dimensional structures with periodicity in only two-dimensions. Jiang. et al. designed a three-dimensional multilayer structure using polyester filaments and ABS plastic tubes filled with polyurethane foam.6 Figure 4 shows the auxetic behaviour of the composite.
In TEAM-A, we want to create truly solid auxetics without using foams or other air-fille materials. One TEAM-A researcher is investigating composite auxetics, where a soft material replaces the air to fabricate a solid material. There has been little research in such composite auxetics, with the majority being theoretical. G. Patil showed the effect of the Young’s modulus of the filler material on the auxetic behaviour. For a composite material to maintain its auxetic behaviour, the Young’s modulus of the filler material must be around 0.5% of the structure.7 TEAM-A intends to fabricate such structures using 3D printing and investigate various filler materials. After developing composite auxetics, we will measure the mechanical properties and the interaction of incident acoustic waves. After performing the initial measurements, we will develop composite structures for sound absorption applications.
Fig. 1. a) A conventional material with a positive Poisson’s ratio undergoing uniaxial compression will experience a transverse expansion b) An auxetic material undergoing the same uniaxial compression will compress in the transverse direction. Grey shows the non-deformed material. Blue shows the material after deformation.
Fig. 2. The initial form of a six-pointed star pore structure and two different deformation mechanisms. Two deformation mechanics are shown: rotational and re-entrant. The figure was adapted from Mizzi.4
Fig. 3. a) 3D bowtie lattice with two different strut angles (a). (b) 3D star lattice. Image is from G. Patil et al. 5
Fig. 4. a) Original composite structure. b) Structure under compression displaying auxetic behaviour and the collapse of some of the ABS rods due to the compression (red circles). This figure is from Jiang et al.5
[1] Evans, K. E., and Alderson, A. “Auxetic materials: functional materials and structures from lateral thinking!.” Advanced materials 12.9 (2000): 617-628.
[2] White, L. “Auxetic foam set for use in smart filters and wound dressings.” Urethanes Technology International 26.4 (2009): 34-36.
[3] Lakes, R. S. “Negative-Poisson’s-ratio materials: auxetic solids.” Annual review of materials research 47 (2017).
[4] Mizzi, L. et al. “Mechanical metamaterials with star-shaped pores exhibiting negative and zero Poisson’s ratio.” Materials & Design 146 (2018): 28-37.
[5] Patil, G. U. et al. “3D auxetic lattice materials for anomalous elastic wave polarization.” Applied Physics Letters 115.9 (2019): 091902.
[6] Jiang, L. et al. “Auxetic composite made with multilayer orthogonal structural reinforcement.” Composite Structures 135 (2016): 23-29.
[7] Patil, G. U., and Matlack, K. H. “Effective property evaluation and analysis of three-dimensional periodic lattices and composites through Bloch-wave homogenization.” The Journal of the Acoustical Society of America 145.3 (2019): 1259-1269.