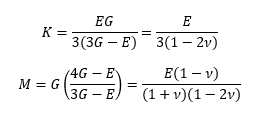Email us


A material of Poisson’s Ratio 0.5 maintains the same volume when stretched. An unstrained cube of length L (dark blue) is placed under tension, leading to a reduction in width but increase in length (pale blue).
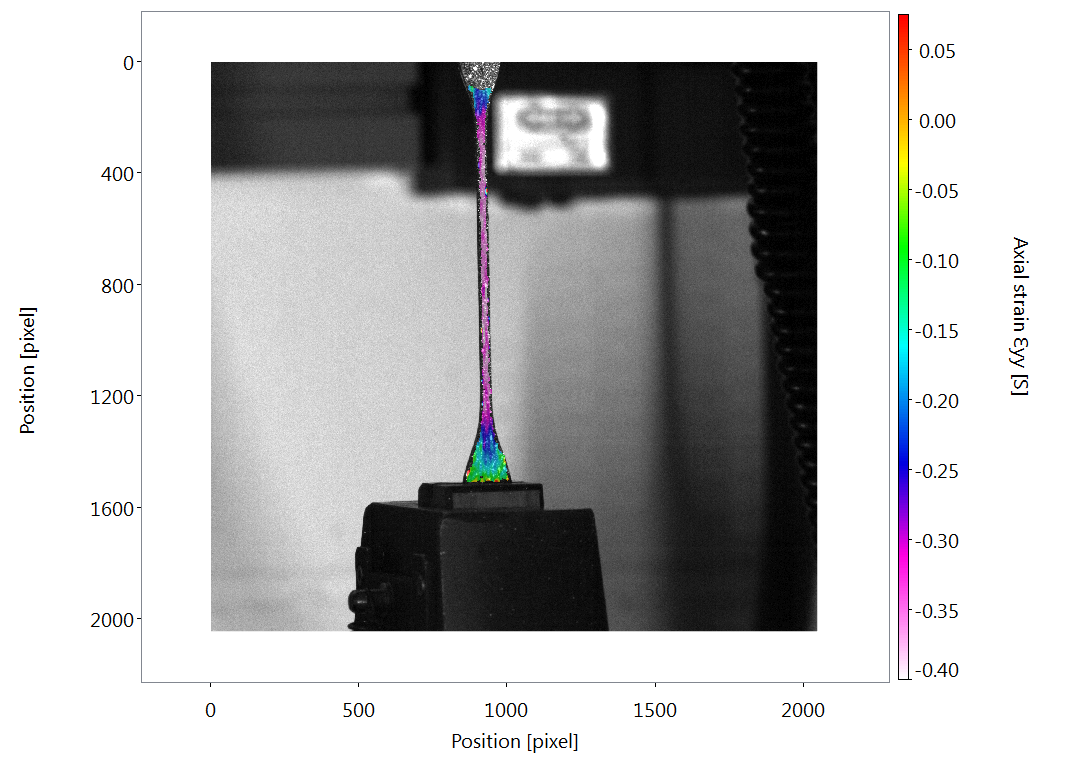
A DIC (Digital Image Correlation) of an elastomeric material under tensile load. The DIC algorithm allows full-field, non-contact measurement of strain by tracking the motion of a pattern applied to the sample surface. Combined with stress data from the machine used to load the sample, dynamic stress-strain behaviour can be determined.
Measuring Poisson’s Ratio: Stretch Targets
Authors: Dr Simon Horsley (University of Exeter) & Prof. Christopher Lawrence (QinetiQ, Farnborough).
The research behind this piece was supported by TEAM-A's Innovation Fund.
One of the key aims of the TEAM-A programme is for the University of Exeter and QinetiQ to reach a point where they can freely share their experts and equipment. This should help everyone to save money (why buy kit that a colleague already has?), provide deeper expertise and experience to customers, and spark some innovative ideas by getting staff from different technical areas to share problems. In this spirit, TEAM-A has recently arranged for Dr Simon Horsley, a Senior Research Fellow in the School of Physics, to spend some time with QinetiQ’s Acoustic Materials Team to analyse a particularly thorny problem.
Characterising the dynamic properties of materials is of fundamental importance to the development of any technologies for noise and vibration control, such as claddings for echo control in concert halls, or vehicle modifications for crew comfort. However, there are certain material types that are very difficult to accurately characterise, a problem recognised in the scientific literature but currently without a solution. This is particularly vexing for the QinetiQ team as their task is to design, characterise and optimise new materials and structures to control the flow of sound and vibration, the best of which are often…. rubbery.
To understand why this is, we first need to define the Poisson effect. Suppose that you are handed a cube of a material: if you place your hands on opposite sides of the cube and squeeze them together then you’d typically expect the cube to expand in the directions of the other four faces, the material ‘squidging out’ as it is compressed. Alternatively, if you pulled two faces away from each other, you’d normally expect the material between to become thinner, in the manner of a stretched elastic band. The ratio of relative contraction to relative expansion is defined to be Poisson’s Ratio (v), a useful value for determining the behaviour of a material when exposed to vibrations, whether they are acoustic or mechanical in origin.
The exact values of v vary according to the type of material under test. Solid and uniform rubbery materials will exhibit values at or near to the maximum of 0.5 as they maintain a near-constant volume when pressure is applied (i.e. they are incompressible), whilst materials that do not tend to expand laterally when compressed (e.g. certain types of cork; some novel honeycomb structures [1]) have a value of 0.0. Most other materials fall somewhere between these two cases, although negative values are also possible, for which a stretched material grows fatter: such materials are defined to be auxetic and are typically constructed artificially with an internal structure that unfolds in an origami-like manner [2], although natural auxetic materials also exist (e.g. skin is a felt of collagen fibres that can grow thicker when stretched at low strain [3]).
Dynamic Mechanical Analysis (DMA) is the ‘workhorse’ technique for characterising the frequency dependent mechanical properties of solid materials. A sinusoidal stress (force over a given area) is applied to a material and the resultant strain (the extension relative to its original length) is measured: if applied in tension (typically via bending mode deformation) then the ratio of stress to strain provides the Young’s Modulus (E), whilst a shear measurement provides the Shear Modulus (G). These two values can subsequently be used to determine v via equations such as 'Equation 1'.
Here, M is the Plane Wave modulus and K is the Bulk Wave Modulus: both are very useful values for any structural modelling exercise, and generally need to be known to a high degree of accuracy in order to achieve realistic predictions. However, there is an immediate problem: if v is 0.5 then the denominator on the right-hand side becomes zero. This means that the calculation of M and K from measured properties of near-incompressible materials (v -> 0.5) can lead to unphysical results where K and M are overestimated by many orders of magnitude. Combined with the fact that even small errors in the DMA calculations of E and G will lead to further large errors in K and M [8], it is difficult to obtain reliable data for the rubbery materials that are so important in acoustic and vibration damping.
This is not a newly described problem. Several papers in the open literature have discussed the issue [4,5,6,7,8,9] but no solutions have yet been proposed. TEAM-A are hence searching for a new approach to the issue, either through mathematics or via an entirely different measurement technique. Early results suggest that a combination of the two may be the best approach, and we are reviewing the various techniques available in the QinetiQ laboratories to determine our options, drawing upon expertise both at the University of Exeter and in QinetiQ.
References:
[1] Jinjin Chen et al, “Zero Poisson’s ratio flexible skin for potential two-dimensional wing morphing”, Aerospace Sci & Tech, 45, (2015), p228-241.
[2] Evans KE et al, “Molecular network design”, Nature, Vol. 353, No. 6340, (1991), p124.
[3] C Lees et al, “Poisson’s ratio in Skin”, Bio-Medical Materials and Engineering, 1, (1991), pp19-23.
[4] T Pritz, “The Poisson’s loss factor of solid viscoelastic materials”, Journal of Sound and Vibration, 306, (2007), pp790-802.
[5] T Pritz, “Measurement methods of complex Poisson’s ratio of viscoelastic materials”, Applied Acoustics, 60, (2000), pp270-292.
[6] T Pritz, “Relation of bulk to shear loss factor of solid viscoelastic materials”, Journal of Sound and Vibration, 324, (2009), pp514-519.
[7] P H Mott et al, “Acoustic and dynamic mechanical properties of a polyurethane rubber”, J. Acoust. Soc. Am., Vol. 111, No.4, April 2002, pp1782-1789.
[8] P H Mott et al, “The bulk modulus and Poisson’s ratio of “incompressible” materials”, Journal of Sound and Vibration, 312, (2008), pp572-575.
[9] N.W. Tschoegl, W.G. Knauss, I. Emri, “Poisson’s ratio in linear viscoelasticity—a critical review”, Mechanics of Time-Dependent Materials, 6, (2002) pp3–51.