Research
Research and impact
Research and impact
Research and impact
Research and impact
Research and impact
Our research encompasses the development of mathematical modelling and data and systems science techniques both on a fundamental level and also with application to grand challenges in energy, environmental, ecological and societal sustainability. Key themes include Systems and Control, Epidemiology and Human Health, Mathematical Biology and Ecology, Renewable Energy, and Mathematics for Innovation and Business. Follow the drop down menus to find out more about the individual themes and their significant outputs.
Systems and Control - Theory, Analysis and Applications
Our research interests in this theme include dynamical systems, control theory and analysis. In particular, the group’s research in dynamical systems include stability, behaviour and performance analysis of linear to nonlinear, infinite-dimensional, switched systems, complex networked and stochastic systems. In control theory, our focus is on optimal, robust, nonlinear, adaptive, stochastic, learning and intelligent control, alongside the development of data-driven and machine learning methodologies in control systems design. This is driven by diverse real-world applications ranging from conservation and ecological management to renewable energy systems. We are also active in complex and functional analysis, fractional calculus and integral transforms, and their connections with signal and image processing, for applications such as neuroscience and cardiology.
Active members and significant achievements
- Dr Tim Hughes has resolved numerous longstanding open questions on the analysis and design of passive systems (i.e., systems that do not consume energy), with application to low energy mechanical design and electric circuit synthesis. His research is now included in the definitive textbooks of the field.
- Dr Markus Mueller and Professor Stuart Townley pioneered the use of adaptive and set-point control for management of natural populations.
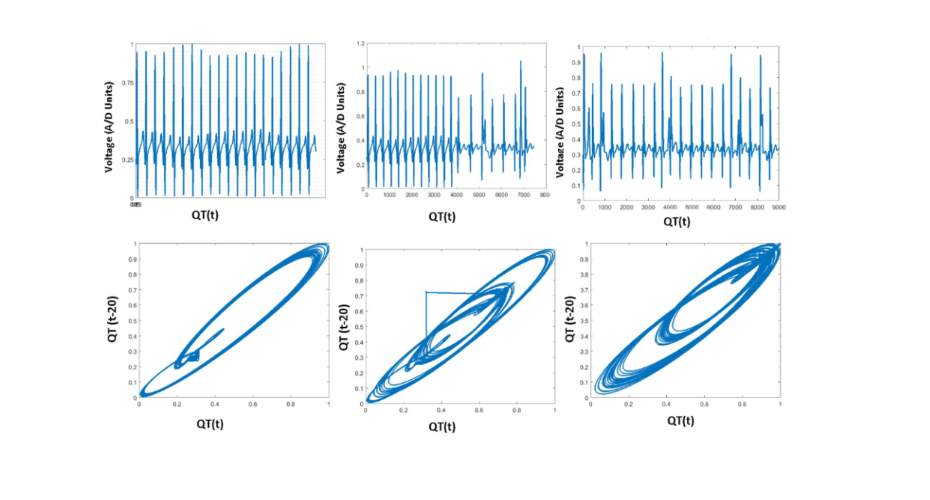
- Dr Saptarshi Das has developed fractional calculus and artificial intelligence based hybrid methods to discover hundreds of new chaotic attractors and to study synchronization of switched chaotic systems.
- Dr Houry Melkonian has used harmonic analysis to study the generalised Fourier-type series that arise in the study of the (p,q)-Laplacian with Dirichlet boundary conditions, and has developed a new stream of research which studies the behaviour of integrals of generalised sinc functions.
- Dr Mark Callaway has research interests in random dynamical systems and bifurcation.
- Guiver, C., Logemann, H. and Townley, S., 2017. Low-gain integral control for multi-input multioutput linear systems with input nonlinearities. IEEE Transactions on Automatic Control, 62(9), pp.4776-4783, doi: https://doi.org/10.1109/TAC.2017.2691301.
- Hughes, T.H., 2020. Minimal series-parallel network realizations of bicubic impedances. IEEE Transactions on Automatic Control, doi: https://doi.org/10.1109/TAC.2020.2968859.
- Hughes, T.H., 2018. On the Optimal Control of Passive or Nonexpansive Systems. IEEE Transactions on Automatic Control, 63(12), pp.4079-4093, doi: https://doi.org/10.1109/TAC.2018.2819656.
- Hughes, T.H., 2017. Why RLC realizations of certain impedances need many more energy storage elements than expected. IEEE Transactions on Automatic Control, 62(9), pp.4333-4346, doi: https://doi.org/10.1109/TAC.2017.2667585.
- Hughes, T.H. and Smith, M.C., 2014. On the minimality and uniqueness of the Bott–Duffin realization procedure. IEEE Transactions on Automatic Control, 59(7), pp.1858-1873, doi: https://doi.org/10.1109/TAC.2014.2312471.
- Hughes, T.H., 2019. On reciprocal systems and controllability. Automatica, 101, pp.396-408, doi: https://doi.org/10.1016/j.automatica.2018.12.021.
- Hughes, T.H., 2017. A theory of passive linear systems with no assumptions. Automatica, 86, pp.87-97, doi: https://doi.org/10.1016/j.automatica.2017.08.017.
- Halder, K., Das, S., Panda, D.K., Das, S. and Gupta, A., 2021. QoS aware joint observer and networked PI/PID controller design using LMIs under specified rate of packet dropouts. Applied Mathematics and Computation, 401, p.126125, doi: https://doi.org/10.1016/j.amc.2021.126125.
- Melkonian, H. and Takeuchi, S., 2021. Remarkable properties of the sincp,q functions and related integrals. Journal of Mathematical Analysis and Applications, 499(1), p.124981, doi: https://doi.org/10.1016/j.jmaa.2021.124981.
- Boulton, L. and Melkonian, H., 2016. Generalised trigonometric functions: Basis and regularity properties, Journal of Mathematical Analysis and Applications, 444(1), pp. 25-46, doi: https://doi.org/10.1016/j.jmaa.2016.06.024.
- Das, S., Pan, I. and Das, S., 2016. Effect of random parameter switching on commensurate fractional order chaotic systems. Chaos, Solitons & Fractals, 91, pp.157-173, doi: https://doi.org/10.1016/j.chaos.2016.05.014.
- Pan, I. and Das, S., 2015. When Darwin meets Lorenz: Evolving new chaotic attractors through genetic programming. Chaos, Solitons & Fractals, 76, pp.141-155, doi: https://doi.org/10.1016/j.chaos.2015.03.017.
- Guiver, C., Hodgson, D. and Townley, S., 2014. Positive state controllability of positive linear systems. Systems & Control Letters, 65, pp.23-29, doi: https://doi.org/10.1016/j.sysconle.2013.12.002.
- Hughes, T.H., Morelli, A. and Smith, M.C., 2019. On a concept of genericity for RLC networks. Systems & Control Letters, 134, p.104562, doi: https://doi.org/10.1016/j.sysconle.2019.104562.
- Hughes, T.H., 2018. On the internal signature and minimal electric network realizations of reciprocal behaviors. Systems & Control Letters, 119, pp.16-22, doi: https://doi.org/10.1016/j.sysconle.2018.06.007.
- Hughes, T.H. and Smith, M.C., 2017. Controllability of linear passive network behaviors. Systems & Control Letters, 101, pp.58-66, doi: https://doi.org/10.1016/j.sysconle.2015.09.011.
- Edmunds, D.E. and Melkonian, H., 2018. Basis and regularity properties of (p, q)-trigonometric functions and the decay of (p, q)-Fourier coefficients. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 474(2210), p.20170548, doi: https://doi.org/10.1098/rspa.2017.0548.
- Bill, A., Guiver, C., Logemann, H. and Townley, S., 2016. Stability of nonnegative Lur'e systems. SIAM Journal on Control and Optimization, 54(3), pp.1176-1211, doi: https://doi.org/10.1137/140994599.
- Hughes, T.H., 2016. Behavioral realizations using companion matrices and the Smith form. SIAM Journal on Control and Optimization, 54(2), pp.845-865, doi: https://doi.org/10.1137/140991911.
- Pan, I., Das, S. and Routh, A., 2015. Towards a global controller design for guaranteed synchronization of switched chaotic systems. Applied Mathematical Modelling, 39(8), pp.2311-2331, doi: https://doi.org/10.1016/j.apm.2014.10.039.
- Pan, I. and Das, S., 2018. Evolving chaos: Identifying new attractors of the generalised Lorenz family. Applied Mathematical Modelling, 57, pp.391-405, doi: https://doi.org/10.1016/j.apm.2018.01.015.
- Guiver, C., Edholm, C., Jin, Y., Mueller, M., Powell, J., Rebarber, R., Tenhumberg, B. and Townley, S., 2016. Simple adaptive control for positive linear systems with applications to pest management. SIAM Journal on Applied Mathematics, 76(1), pp.238-275, doi: https://doi.org/10.1137/140996926.
Epidemiology and Human Health
Our research interests in this theme include complex systems, data science and statistical modelling approaches to resolve big research questions in epidemiology and human health. Within epidemiology and infectious disease modelling, a particular focus is on dengue, malaria and antimicrobial resistance. Within human health data analytics and modelling, we focus on digital technologies, artificial intelligence and machine learning methods for health and well-being, alongside computational problems in neuroscience and cardiology.
Active members and significant achievements
- Dr Mario Recker and collaborators made fundamental contributions to a World Health Organisation (WHO) model comparison study on the safety and long-term impact of the first dengue vaccine. He is also active in statistical modelling using individual based models of vector-borne disease systems and immune signature data classification for malaria.
- Dr Markus Mueller and Professor Stuart Townley are theme-leads for modelling of systems design in Smartline and Smartline 2.0, two interdisciplinary projects that explore the relationship between digital technology, health and well-being through research and collaborations with local businesses and social enterprises. Professor Townley and collaborators also developed AI-based tools for predicting the development of acute kidney injury on hospital admission.
- Dr Saptarshi Das and collaborators developed electroencephalogram (EEG), functional magnetic resonance imaging (fMRI), and diffusion tensor imaging (DTI) data processing and assimilation algorithms for studying phase synchronization and functional brain connectivity in autism and anxiety. Dr Das also works on computational challenges in cardiac and neural signal processing using nonlinear dynamics, stochastic processes and machine learning.
- Laabei, M., Recker, M., Rudkin, J.K., Aldeljawi, M., Gulay, Z., Sloan, T.J., Williams, P., Endres, J.L., Bayles, K.W., Fey, P.D. and Yajjala, V.K., 2014. Predicting the virulence of MRSA from its genome sequence. Genome Research, 24(5), pp.839-849, doi: http://www.genome.org/cgi/doi/10.1101/gr.165415.113.
- Holding, T., Valletta, J.J. and Recker, M., 2018. Multiscale Immune Selection and the Transmission-Diversity Feedback in Antigenically Diverse Pathogen Systems. The American Naturalist, 192(6), pp.E189-E201, doi: https://doi.org/10.1086/699535.
- Talavera-López, C., Bediako, Y., Lin, J.W., Valletta, J.J., Recker, M. and Langhorne, J., 2019. Comparison of whole blood and spleen transcriptional signatures over the course of an experimental malaria infection. Scientific Reports, 9(1), pp.1-12, doi: https://doi.org/10.1038/s41598-019-52388-y.
- Vemishetty, N., Gunukula, R.L., Acharyya, A., Puddu, P.E., Das, S. and Maharatna, K., 2019. Phase Space Reconstruction Based CVD Classifier Using Localized Features. Scientific Reports, 9(1), pp.1-18, doi: https://doi.org/10.1038/s41598-019-51061-8.
- Recker, M., Vannice, K., Hombach, J., Jit, M. and Simmons, C.P., 2016. Assessing dengue vaccination impact: Model challenges and future directions. Vaccine, 34(38), pp.4461-4465, doi: https://doi.org/10.1016/j.vaccine.2016.06.082.
- Valletta, J.J. and Recker, M., 2017. Identification of immune signatures predictive of clinical protection from malaria. PLoS Computational Biology, 13(10), p.e1005812, doi: https://doi.org/10.1371/journal.pcbi.1005812.
- Jamal, W., Das, S., Maharatna, K., Pan, I. and Kuyucu, D., 2015. Brain connectivity analysis from EEG signals using stable phase-synchronized states during face perception tasks. Physica A: Statistical Mechanics and its Applications, 434, pp.273-295, doi: https://doi.org/10.1016/j.physa.2015.03.087.
- Bono, V., Das, S., Jamal, W. and Maharatna, K., 2016. Hybrid wavelet and EMD/ICA approach for artifact suppression in pervasive EEG. Journal of Neuroscience Methods, 267, pp.89-107, doi: https://doi.org/10.1016/j.jneumeth.2016.04.006.
- Bono, V., Jamal, W., Das, S. and Maharatna, K., 2014, May. Artifact reduction in multichannel pervasive EEG using hybrid WPT-ICA and WPT-EMD signal decomposition techniques. In 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 5864-5868). IEEE, doi: https://doi.org/10.1109/ICASSP.2014.6854728.
- Silva-Filho, J.L., Lacerda, M.V., Recker, M., Wassmer, S.C., Marti, M. and Costa, F.T., 2020. Plasmodium vivax in Hematopoietic Niches: Hidden and Dangerous. Trends in Parasitology, doi: https://doi.org/10.1016/j.pt.2020.03.002.
- Jamal, W., Das, S., Oprescu, I.A. and Maharatna, K., 2014. Prediction of synchrostate transitions in EEG signals using Markov chain models. IEEE Signal Processing Letters, 22(2), pp.149-152, doi: https://doi.org/10.1109/LSP.2014.2352251.
- Heiny, S.R., Pautz, S., Recker, M. and Przyborski, J.M., 2014. Protein traffic to the Plasmodium falciparum apicoplast: evidence for a sorting branch point at the Golgi. Traffic, 15(12), pp.1290-1304, doi: https://doi.org/10.1111/tra.12226.
- Holding, T. and Recker, M., 2015. Maintenance of phenotypic diversity within a set of virulence encoding genes of the malaria parasite Plasmodium falciparum. Journal of the Royal Society Interface, 12(113), p.20150848, doi: https://doi.org/10.1098/rsif.2015.0848.
- Tennant, W. and Recker, M., 2018. Robustness of the reproductive number estimates in vector-borne disease systems. PLoS Neglected Tropical Diseases, 12(12), p.e0006999, doi: https://doi.org/10.1371/journal.pntd.0006999.
- Lourenço, J. and Recker, M., 2014. The 2012 Madeira dengue outbreak: epidemiological determinants and future epidemic potential. PLoS Neglected Tropical Diseases, 8(8), doi: https://doi.org/10.1371/journal.pntd.0003083.
- Koulaouzidis, G., Das, S., Cappiello, G., Mazomenos, E.B., Maharatna, K., Puddu, P.E. and Morgan, J.M., 2015. Prompt and accurate diagnosis of ventricular arrhythmias with a novel index based on phase space reconstruction of ECG. International Journal of Cardiology, 182, pp.38-43, doi: https://doi.org/10.1016/j.ijcard.2014.12.067.
- Jamal, W., Das, S., Oprescu, I.A., Maharatna, K., Apicella, F. and Sicca, F., 2014. Classification of autism spectrum disorder using supervised learning of brain connectivity measures extracted from synchrostates. Journal of Neural Engineering, 11(4), p.046019, doi: https://doi.org/10.1088/1741-2560/11/4/046019.
- Cappiello, G., Das, S., Mazomenos, E.B., Maharatna, K., Koulaouzidis, G., Morgan, J. and Puddu, P.E., 2014. A statistical index for early diagnosis of ventricular arrhythmia from the trend analysis of ECG phase-portraits. Physiological Measurement, 36(1), p.107, doi: https://doi.org/10.1088/0967-3334/36/1/107.
- Lourenço, J., Tennant, W., Faria, N.R., Walker, A., Gupta, S. and Recker, M., 2018. Challenges in dengue research: A computational perspective. Evolutionary Applications, 11(4), pp.516-533, doi: https://doi.org/10.1111/eva.12554.
- Recker, M., Laabei, M., Toleman, M.S., Reuter, S., Saunderson, R.B., Blane, B., Török, M.E., Ouadi, K., Stevens, E., Yokoyama, M. and Steventon, J., 2017. Clonal differences in Staphylococcus aureus bacteraemia-associated mortality. Nature Microbiology, 2(10), pp.1381-1388, doi: https://doi.org/10.1038/s41564-017-0001-x.
- Argyropoulos, A., Townley, S., Upton, P.M., Dickinson, S. and Pollard, A.S., 2019. Identifying on admission patients likely to develop acute kidney injury in hospital. BMC Nephrology, 20(1), p.56, doi: https://doi.org/10.1186/s12882-019-1237-x.
- Naik, P.A., Yavuz, M., Qureshi, S., Zu, J., and Townley, S., 2020. Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan. European Physical Journal Plus, 135, p. 795, doi: https://doi.org/10.1140/epjp/s13360-020-00819-5.
Mathematical Biology and Ecology
Research interests within this theme include modelling of ecological dynamics and biological processes in nature.
Active members and significant achievements
- Dr Mario Recker developed a modelling framework to predict individual-level risk of mortality following a bloodstream infection with the hospital superbug staphylococcus aureus (MRSA). He also developed computational algorithms to study a notable male-female health-survival paradox in drosophila. In addition, he has made fundamental contributions in the study of antimicrobial resistance for two antibiotics, gentamicin and kanamycin, for Escherichia coli.
- Dr Markus Mueller and Professor Stuart Townley have pioneered the development of robust control tools for the management of natural populations. They have also developed a mathematical theory for analysing transient dynamics in human, animal and plant population models. This theory has recently been applied to predicting invasion by species into non-native ranges, based on their native demographies. Dr Townley used data science tools to study global patterns of sex and age-variation in seabirds, and has contributed to the development of stochastic projection matrix models for studying demographic dynamics of plant population growth.
- Dr Saptarshi Das has developed image processing algorithms for the statistical characterisation of microbial community pattern formation from scanning electron microscopy images for wild pseudomonas biofilms. Together with collaborators, he has also developed novel statistical feature and wavelet transform based pattern recognition algorithms for plant electrical signal processing to identify chemical pollutants in the environment.
- Jelbert, K., Buss, D., McDonald, J., Townley, S., Franco, M., Stott, I., Jones, O., Salguero-Gómez, R., Buckley, Y., Knight, T. and Silk, M., Sargent, F., Rolph, S., Wilson, P., and Hodgson, D., 2019. Demographic amplification is a predictor of invasiveness among plants. Nature Communications, 10(1), pp.1-6, doi: https://doi.org/10.1038/s41467-019-13556-w.
- Archer, C.R., Recker, M., Duffy, E. and Hosken, D.J., 2018. Intralocus sexual conflict can resolve the male-female health-survival paradox. Nature Communications, 9(1), p.5048, doi: https://doi.org/10.1038/s41467-018-07541-y.
- Dutta Sinha, S., Das, S., Tarafdar, S. and Dutta, T., 2017. Monitoring of Wild Pseudomonas Biofilm Strain Conditions Using Statistical Characterization of Scanning Electron Microscopy Images. Industrial & Engineering Chemistry Research, 56(34), pp.9496-9512, doi: https://doi.org/10.1021/acs.iecr.7b01106.
- Gianuca, D., Phillips, R.A., Townley, S. and Votier, S.C., 2017. Global patterns of sex-and age-specific variation in seabird bycatch. Biological Conservation, 205, pp.60-76, doi: https://doi.org/10.1016/j.biocon.2016.11.028.
- Chatterjee, S.K., Das, S., Maharatna, K., Masi, E., Santopolo, L., Colzi, I., Mancuso, S. and Vitaletti, A., 2017. Comparison of decision tree based classification strategies to detect external chemical stimuli from raw and filtered plant electrical response. Sensors and Actuators B: Chemical, 249, pp.278-295, doi: https://doi.org/10.1016/j.snb.2017.04.071.
- McDonald, J.L., Stott, I., Townley, S. and Hodgson, D.J., 2016. Transients drive the demographic dynamics of plant populations in variable environments. Journal of Ecology, 104(2), pp.306-314, doi: https://doi.org/10.1111/1365-2745.12528.
- Kuijper, B., Johnstone, R.A. and Townley, S., 2014. The evolution of multivariate maternal effects. PLoS Computational Biology, 10(4), doi: https://doi.org/10.1371/journal.pcbi.1003550.
- Klümper, U., Recker, M., Zhang, L., Yin, X., Zhang, T., Buckling, A. and Gaze, W.H., 2019. Selection for antimicrobial resistance is reduced when embedded in a natural microbial community. The ISME Journal, 13(12), pp.2927-2937, doi: https://doi.org/10.1038/s41396-019-0483-z.
- Gianuca, D., Votier, S.C., Pardo, D., Wood, A.G., Sherley, R.B., Ireland, L., Choquet, R., Pradel, R., Townley, S., Forcada, J., Tuck, G.N., and Phillips, R.A., 2019. Sex‐specific effects of fisheries and climate on the demography of sexually dimorphic seabirds. Journal of Animal Ecology, 88(9), pp.1366-1378, doi: https://doi.org/10.1111/1365-2656.13009.
- Guiver, C., Packman, D. and Townley, S., 2017. A necessary condition for dispersal driven growth of populations with discrete patch dynamics. Journal of Theoretical Biology, 424, pp.11-25, doi: https://doi.org/10.1016/j.jtbi.2017.03.030.
- Edholm, C.J., Tenhumberg, B., Guiver, C., Jin, Y., Townley, S. and Rebarber, R., 2018. Management of invasive insect species using optimal control theory. Ecological Modelling, 381, pp.36-45, doi: https://doi.org/10.1016/j.ecolmodel.2018.04.011.
- Chatterjee, S.K., Das, S., Maharatna, K., Masi, E., Santopolo, L., Mancuso, S. and Vitaletti, A., 2015. Exploring strategies for classification of external stimuli using statistical features of the plant electrical response. Journal of the Royal Society Interface, 12(104), p.20141225, doi: https://doi.org/10.1098/rsif.2014.1225.
- Gates, D.E., Valletta, J.J., Bonneaud, C. and Recker, M., 2018. Quantitative host resistance drives the evolution of increased virulence in an emerging pathogen. Journal of Evolutionary Biology, 31(11), pp.1704-1714, doi: https://doi.org/10.1111/jeb.13366.
- Das, S., Ajiwibawa, B.J., Chatterjee, S.K., Ghosh, S., Maharatna, K., Dasmahapatra, S., Vitaletti, A., Masi, E. and Mancuso, S., 2015. Drift removal in plant electrical signals via IIR filtering using wavelet energy. Computers and Electronics in Agriculture, 118, pp.15-23, doi: https://doi.org/10.1016/j.compag.2015.08.013.
- Guiver, C., Mueller, M., Hodgson, D. and Townley, S., 2016. Robust set-point regulation for ecological models with multiple management goals. Journal of Mathematical Biology, 72(6), pp.1467-1529, doi: https://doi.org/10.1007/s00285-015-0919-7.
- Guiver, C., Logemann, H., Rebarber, R., Bill, A., Tenhumberg, B., Hodgson, D. and Townley, S., 2015. Integral control for population management. Journal of Mathematical Biology, 70(5), pp.1015-1063, doi: https://doi.org/10.1007/s00285-014-0789-4.
- Guiver, C., Dreiwi, H., Filannino, D.M., Hodgson, D., Lloyd, S. and Townley, S., 2015. The role of population inertia in predicting the outcome of stage-structured biological invasions. Mathematical Biosciences, 265, pp.1-11, doi: https://doi.org/10.1016/j.mbs.2015.04.005.
- Eager, E.A., Guiver, C., Hodgson, D., Rebarber, R., Stott, I. and Townley, S., 2014. Bounds on the dynamics of sink populations with noisy immigration. Theoretical Population Biology, 92, pp.88-96, doi: https://doi.org/10.1016/j.tpb.2013.12.004.
- Chatterjee, S.K., Ghosh, S., Das, S., Manzella, V., Vitaletti, A., Masi, E., Santopolo, L., Mancuso, S. and Maharatna, K., 2014. Forward and inverse modelling approaches for prediction of light stimulus from electrophysiological response in plants. Measurement, 53, pp.101-116, doi: https://doi.org/10.1016/j.measurement.2014.03.040.
- Nicol-Harper, A., Dooley, C., Packman, D., Mueller, M., Bijak, J., Hodgson, D., Townley, S. and Ezard, T., 2018. Inferring transient dynamics of human populations from matrix non-normality. Population Ecology, 60(1), pp.185-196, doi: https://doi.org/10.1007/s10144-018-0620-y.
- McDonald, J.L., Franco, M., Townley, S., Ezard, T.H., Jelbert, K. and Hodgson, D.J., 2017. Divergent demographic strategies of plants in variable environments. Nature Ecology & Evolution, 1(2), pp.1-6, doi: https://doi.org/10.1038/s41559-016-0029.
- Elragig, A., Townley, S. and Dreiwi, H., 2014. On a Negative Relation between Bacterial Taxis and Turing Pattern Formation. International Journal of Bioengineering and Life Sciences, 8(8), pp.834-838, doi: https://doi.org/10.5281/zenodo.1094283.
Renewable Energy, Sustainability and Fluid Mechanics
Our research in this theme involves collaboration with the world-class Renewable Energy group and the Exeter Energy network. In particular, Drs Hamid Alemi Ardakani, Markus Mueller, Saptarshi Das and Professor Stuart Townley are active in modelling and design of wave energy converters and smart grids; energy data analytics and machine learning; and data driven modelling, control and optimization of renewable and sustainable energy systems.
Active members and significant achievements
- Dr Markus Mueller works on modelling and control design for marine renewable technologies. He led the control design work package for OPERA, an EU Horizon 2020 Research and Innovation programme grant aimed at technology readiness for oscillating water column wave energy converters. He also developed spatio-temporal life cycle analysis methods to determine localised emissions and wind energy over time. In addition, Dr Mueller works on control strategies of ocean wave converters, turbines and wave power plants.
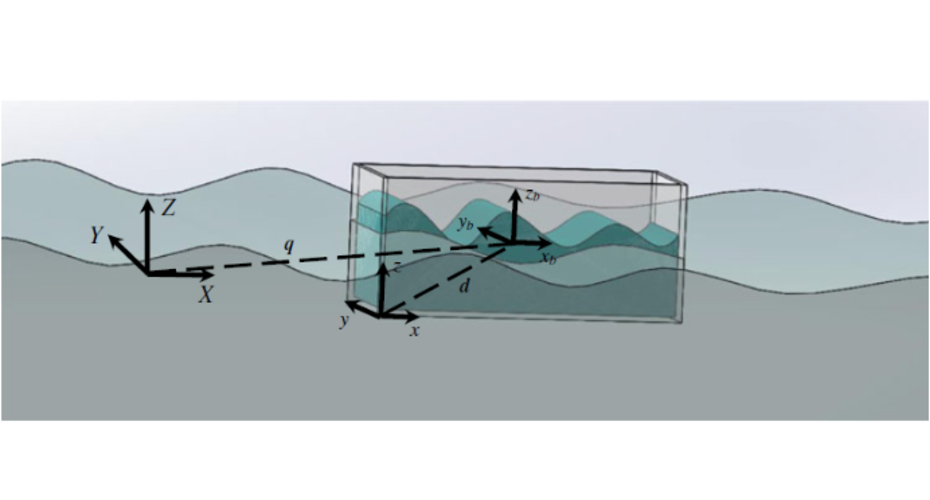
- Dr Alemi Ardakani has research interests in mathematical analysis, numerical analysis, structure-preserving algorithm design, and theoretical fluid and continuum mechanics. He has recently developed new variational principles for the generalized Green-Naghdi and Whitham equations, and Euler-Poincare variational principles for three-dimensional interactions between ocean surface waves and a floating rigid-body, dynamically coupled to its interior fluid sloshing.
- Dr Saptarshi Das works on energy and power systems dynamics, control, optimization and data analytics with a focus on clean energy and sustainable technologies. In two recent highly cited papers, he developed fractional calculus based intelligent control approach using chaotic swarm optimization and surrogate based optimization for hybrid power systems and microgrids with renewable generation and energy storage. Dr Das also used robust optimization and kriging based surrogate models to handle complexity of load and renewable generation patterns for distributed networked control of energy storage elements in smart grids, and he has also developed chaotic multi-objective optimization based load frequency fractional order control methods for interconnected power systems. Dr Das is currently using machine learning and artificial intelligence approaches for the development of battery management algorithms in smart grids, in particular islanded micro-grids with solar photovoltaics. This research is making economic impact through the Cornwall New Energy project.
- Alemi Ardakani, H., Bridges, T.J. and Turner, M.R., 2016. Shallow-water sloshing in a moving vessel with variable cross-section and wetting–drying using an extension of George's well-balanced finite volume solver. Journal of Computational Physics, 314, pp.590-617, doi: https://doi.org/10.1016/j.jcp.2016.03.037.
- Alemi Ardakani, H., 2019. A variational principle for three-dimensional interactions between water waves and a floating rigid body with interior fluid motion. Journal of Fluid Mechanics, 866, pp.630-659, doi: https://doi.org/10.1017/jfm.2019.107.
- Alemi Ardakani, H., 2017. A coupled variational principle for 2D interactions between water waves and a rigid body containing fluid. Journal of Fluid Mechanics, 827, doi: https://doi.org/10.1017/jfm.2017.517.
- Faÿ, F.X., Henriques, J.C., Kelly, J., Mueller, M., Abusara, M., Sheng, W. and Marcos, M., 2020. Comparative assessment of control strategies for the biradial turbine in the Mutriku OWC plant. Renewable Energy, 146, pp.2766-2784, doi; https://doi.org/10.1016/j.renene.2019.08.074.
- Maier, M., Mueller, M. and Yan, X., 2017. Introducing a localised spatio-temporal LCI method with wheat production as exploratory case study. Journal of Cleaner Production, 140, pp.492-501, doi: https://doi.org/10.1016/j.jclepro.2016.07.160.
- Pan, I. and Das, S., 2016. Fractional order AGC for distributed energy resources using robust optimization. IEEE Transactions on Smart Grid, 7(5), pp.2175-2186, doi: https://doi.org/10.1109/TSG.2015.2459766.
- Pan, I. and Das, S., 2015. Kriging based surrogate modeling for fractional order control of microgrids. IEEE Transactions on Smart Grid, 6(1), pp.36-44, doi: https://doi.org/10.1109/TSG.2014.2336771.
- Pan, I. and Das, S., 2015. Fractional-order load-frequency control of interconnected power systems using chaotic multi-objective optimization. Applied Soft Computing, 29, pp.328-344, doi: https://doi.org/10.1016/j.asoc.2014.12.032.
- Alemi Ardakani, H., Bridges, T.J., Gay-Balmaz, F., Huang, Y.H. and Tronci, C., 2019. A variational principle for fluid sloshing with vorticity, dynamically coupled to vessel motion. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 475(2224), p.20180642, doi: https://doi.org/10.1098/rspa.2018.0642.
- Alemi Ardakani, H., Bridges, T.J. and Turner, M.R., 2016. Adaptation of f-wave finite volume methods to the two-layer shallow-water equations in a moving vessel with a rigid-lid. Journal of Computational and Applied Mathematics, 296, pp.462-479, doi: https://doi.org/10.1016/j.cam.2015.09.026.
- Alemi Ardakani, H., 2016. A symplectic integrator for dynamic coupling between nonlinear vessel motion with variable cross-section and bottom topography and interior shallow-water sloshing. Journal of Fluids and Structures, 65, pp.30-43, doi: https://doi.org/10.1016/j.jfluidstructs.2016.03.013.
- Alemi Ardakani, H., Bridges, T.J. and Turner, M.R., 2015. Dynamic coupling between horizontal vessel motion and two-layer shallow-water sloshing. Journal of Fluids and Structures, 59, pp.432-460, doi: https://doi.org/10.1016/j.jfluidstructs.2015.10.002.
- Turner, M.R., Alemi Ardakani, H. and Bridges, T.J., 2015. Instability of sloshing motion in a vessel undergoing pivoted oscillations. Journal of Fluids and Structures, 52, pp.166-180, doi: https://doi.org/10.1016/j.jfluidstructs.2014.10.012.
- Turner, M.R., Bridges, T.J. and Alemi Ardakani, H., 2015. The pendulum-slosh problem: Simulation using a time-dependent conformal mapping. Journal of Fluids and Structures, 59, pp.202-223, doi: https://doi.org/10.1016/j.jfluidstructs.2015.09.007.
- Panda, D.K., Das, S. and Townley, S., 2020. Toward a More Renewable Energy-Based LFC Under Random Packet Transmissions and Delays With Stochastic Generation and Demand. IEEE Transactions on Automation Science and Engineering, doi: https://doi.org/10.1109/TASE.2020.3042570.
- Maier, M., Mueller, M. and Yan, X., 2017. Introduction of a spatiotemporal Life Cycle Inventory method using a wind energy example. Energy Procedia, 142, pp.3035-3040, doi: https://doi.org/10.1016/j.egypro.2017.12.441.
- Pan, I. and Das, S., 2016. Fractional order fuzzy control of hybrid power system with renewable generation using chaotic PSO. ISA Transactions, 62, pp.19-29, doi: https://doi.org/10.1016/j.isatra.2015.03.003.
- Alemi Ardakani, H., 2020. An alternative view on the Bateman–Luke variational principle. European Journal of Mechanics-B/Fluids, doi: https://doi.org/10.1016/j.euromechflu.2020.02.008.
- Alemi Ardakani, H., 2016. Adaptation of f-wave finite volume methods to the Boonkasame–Milewski non-Boussinesq two-layer shallow interfacial sloshing equations coupled to the vessel motion. European Journal of Mechanics-B/Fluids, 60, pp.33-47, doi: https://doi.org/10.1016/j.euromechflu.2016.04.012.
- Turner, M.R., Bridges, T.J. and Alemi Ardakani, H., 2017. Lagrangian particle path formulation of multilayer shallow-water flows dynamically coupled to vessel motion. Journal of Engineering Mathematics, 106(1), pp.75-106, doi: https://doi.org/10.1007/s10665-016-9893-3.
- Alemi Ardakani, H. and Turner, M.R., 2016. Numerical simulations of dynamic coupling between shallow-water sloshing and horizontal vessel motion with baffles. Fluid Dynamics Research, 48(3), p.035504, doi: https://doi.org/10.1088/0169-5983/48/3/035504.
- Abaiee, M.M., Ketabdari, M.J., Ahmadi, A. and Alemi Ardakani, H., 2016. Numerical and experimental study on the dynamic behavior of a sea-star tension leg platform against regular waves. Journal of Applied Mechanics and Technical Physics, 57(3), pp.510-517, doi: https://doi.org/10.1134/S0021894416030159.
Mathematics for Innovation and Business
Within this theme, our focus is to develop mathematical, statistical and computational methods and tools needed for sustainable growth of small and medium size business, working with the energy sector, mining, renewable energy trading, industrial and domestic waste management, and other public and charity sector organisations focussed on conservation ecology and environmental sustainability.
Active members and significant achievements
- Dr Markus Mueller and Professor Stuart Townley have completed two Knowledge Transfer Partnerships (KTP) with NJW Ltd. In the built environment and with Hirst Magnetic Instruments Ltd. on magnet characterisation. Drs Saptarshi Das and TJ McKinley are currently collaborating in a KTP with Chelonia Ltd. on data analytics and statistical modelling for marine-life monitoring. The centre also hosts two industry-funded PhD project students.
- Through the projects Marine-i, Smartline and Tevi, the group has established substantive engagement with regional SMEs. In Tevi, Dr Markus Mueller leads the electric vehicle charging network challenge, which draws on multi-objective optimisation methods to enable the decarbonisation of transport in Cornwall. In Smartline, Dr Mueller works with Buzz Interactive Ltd. on the development of a self-assessment and assistance application for Meniere’s Disease.
- Dr Saptarshi Das works on seismic data processing, imaging and fast computational and statistical methods for geophysical inversion, relevant for the oil and gas, mining and carbon capture and storage industries. Recently Dr Das and collaborators have developed statistical pattern recognition algorithms for field emission scanning electron microscope (FESEM) images to study crystal growth modelling in complex biopolymers, with has potential impact in pharmaceuticals. Dr Das and collaborators have also developed artificial intelligence based predictive models for fluidized bed reactors from experimental data for solid waste management. In addition, Dr Das used multi-objective optimization methods to resolve control conflicts to study design trade-offs in automatic voltage control of synchronous generators in power plants. He has also recently developed several time delay handling methods relevant for process control and industrial automation to obtain stability regions for designing robust stabilizing controllers using random search, optimization and sampling approach in fusion with unsupervised machine learning for identifying the robust stable solutions amongst many conflicting control objectives. Drs Tim Hughes and Saptarshi Das have interests in financial systems modelling with deterministic and stochastic models using dynamical systems theory and time series forecasting methods using machine learning and statistical signal processing approaches.
- Pandey, D.S., Pan, I., Das, S., Leahy, J.J. and Kwapinski, W., 2015. Multi-gene genetic programming based predictive models for municipal solid waste gasification in a fluidized bed gasifier. Bioresource Technology, 179, pp.524-533, doi: https://doi.org/10.1016/j.biortech.2014.12.048.
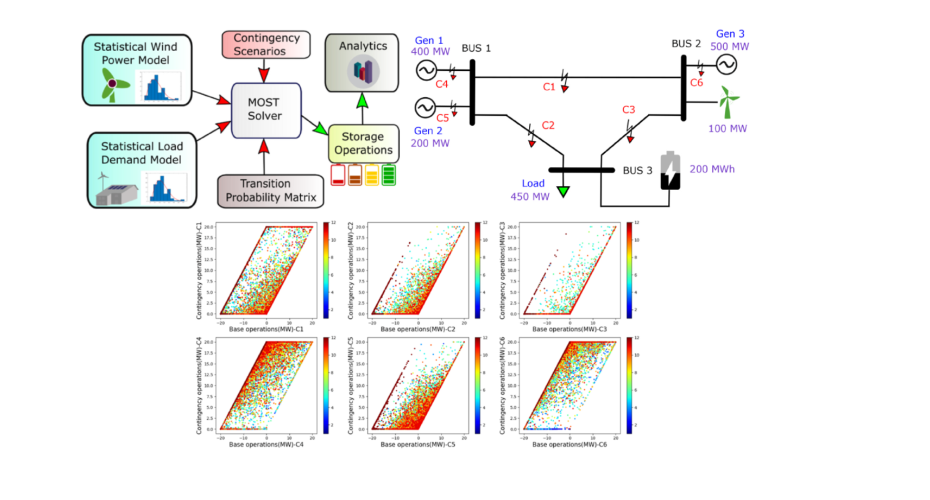
- Panda, D.K. and Das, S., 2020. Economic operational analytics for energy storage placement at different grid locations and contingency scenarios with stochastic wind profiles. Renewable and Sustainable Energy Reviews, p.110474, doi: https://doi.org/10.1016/j.rser.2020.110474.
- Dutta Choudhury, M., Das, S., Roy, B., Sengupta, S., Tarafdar, S. and Karmakar, S., 2019. Salt crystal growth in interacting drops of a complex biopolymer: Statistical characterization using FESEM images. Chemical Engineering Science, 207, pp.1121-1139, doi: https://doi.org/10.1016/j.ces.2019.07.037.
- Das, S., Chen, X., Hobson, M.P., Phadke, S., van Beest, B., Goudswaard, J. and Hohl, D., 2018. Surrogate regression modelling for fast seismogram generation and detection of microseismic events in heterogeneous velocity models. Geophysical Journal International, 215(2), pp.1257-1290, doi: https://doi.org/10.1093/gji/ggy283.
- Pandey, D.S., Das, S., Pan, I., Leahy, J.J. and Kwapinski, W., 2016. Artificial neural network based modelling approach for municipal solid waste gasification in a fluidized bed reactor. Waste Management, 58, pp.202-213, doi: https://doi.org/10.1016/j.wasman.2016.08.023.
- Acharya, A., Das, S., Pan, I. and Das, S., 2014. Extending the concept of analog Butterworth filter for fractional order systems. Signal Processing, 94, pp.409-420, doi: https://doi.org/10.1016/j.sigpro.2013.07.012.
- Das, S., Halder, K. and Gupta, A., 2020. Delay Handling Method in Dominant Pole Placement based PID Controller Design. IEEE Transactions on Industrial Informatics, 16(2), pp.980-991, doi: https://doi.org/10.1109/TII.2019.2918252.
- Das, S. and Pan, I., 2014. On the Mixed H2/H∞ Loop-Shaping Tradeoffs in Fractional-Order Control of the AVR System. IEEE Transactions on Industrial Informatics, 10(4), pp.1982-1991, doi: https://doi.org/10.1109/TII.2014.2322812.
- Halder K., Das S., and Gupta A., 2020. Time delay handling in dominant pole placement with PID controllers to obtain stability regions using random sampling. International Journal of Control, doi: https://doi.org/10.1080/00207179.2020.1764110.
- Das, S., Halder, K. and Gupta, A., 2018. Performance analysis of robust stable PID controllers using dominant pole placement for SOPTD process models. Knowledge-Based Systems, 146, pp.12-43, doi: https://doi.org/10.1016/j.knosys.2018.01.030.
- Pan, I., Das, S. and Das, S., 2015. Multi-objective active control policy design for commensurate and incommensurate fractional order chaotic financial systems. Applied Mathematical Modelling, 39(2), pp.500-514, doi: https://doi.org/10.1016/j.apm.2014.06.005.
- Das, S., Pan, I. and Das, S., 2015. Multi-objective LQR with optimum weight selection to design FOPID controllers for delayed fractional order processes. ISA Transactions, 58, pp.35-49, doi: https://doi.org/10.1016/j.isatra.2015.06.002.
- Pakhira, A., Das, S., Pan, I. and Das, S., 2015. Symbolic representation for analog realization of a family of fractional order controller structures via continued fraction expansion. ISA Transactions, 57, pp.390-402, doi: https://doi.org/10.1016/j.isatra.2015.01.007.
- Chen, X., Hobson, M., Das, S. and Gelderblom, P., 2019. Improving the efficiency and robustness of nested sampling using posterior repartitioning. Statistics and Computing, 29(4), pp.835-850, doi: https://doi.org/10.1007/s11222-018-9841-3.
- Halder, K., Das, S. and Gupta, A., 2020. Transformation of LQR Weights for Discretization Invariant Performance of PI/PID Dominant Pole Placement Controllers. Robotica, 38(2), pp.271-298, doi: https://doi.org/10.1017/S0263574719000596.
- Robayo, M., Abusara, M., Mueller, M. and Sharkh, S., 2020, June. A Smart Energy Management System for Battery-Supercapacitor in Electric Vehicles based on the Discrete Wavelet Transform and Deep Learning. In 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE) (pp. 9-14). IEEE, doi: https://doi.org/10.1109/ISIE45063.2020.9152559.
- Das, S., Chen, X. and Hobson, M.P., 2017. Fast GPU-Based seismogram simulation from microseismic events in marine environments using heterogeneous velocity models. IEEE Transactions on Computational Imaging, 3(2), pp.316-329, doi: https://doi.org/10.1109/TCI.2017.2654127.
- Das, S. and Halder, K., 2014, February. Missile attitude control via a hybrid LQG-LTR-LQI control scheme with optimum weight selection. In 2014 First International Conference on Automation, Control, Energy and Systems (ACES) (pp. 1-6). IEEE, doi: https://doi.org/10.1109/ACES.2014.6807996.
- Das, S., Hobson, M.P., Feroz, F., Chen, X., Phadke, S., Goudswaard, J. and Hohl, D., 2021. Microseismic event detection in large heterogeneous velocity models using Bayesian multimodal nested sampling. Data-Centric Engineering, 2, doi: https://doi.org/10.1017/dce.2021.1.
- Panda, D.K. and Das, S., 2019, August. Regression analysis of grid stability under decentralized control. In 2019 International Conference on Engineering, Science, and Industrial Applications (ICESI) (pp. 1-6). IEEE, doi: https://doi.org/10.1109/ICESI.2019.8863027.
- Sinclair, C. and Das, S., 2021, January. Traffic Accidents Analytics in UK Urban Areas using k-means Clustering for Geospatial Mapping. In 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET) (pp. 1-7). IEEE, doi: https://doi.org/10.1109/SeFet48154.2021.9375817.
- Ghosh, S., Panda, D.K., Das, S. and Chatterjee, D., 2021, January. Cross-Correlation Based Classification of Electrical Appliances for Non-Intrusive Load Monitoring. In 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET) (pp. 1-6). IEEE, doi: https://doi.org/10.1109/SeFet48154.2021.9375687.